Perbandingan Trigonometri Sudut-Sudut Istimewa

Sudut istimewa atau biasa juga disebut sudut khusus adalah sudut-sudut yang nilai perbandingan trigonometrinya dapat ditentukan tanpa harus menggunakan alat bantu (seperti kalkulator dan tabel trigonometri). Sudut-sudut istimewa tersebut adalah $0°$, $30°$, $45°$, $60°$, dan $90°$. Nilai-nilai sudut-sudut istimewa ini sering kita jumpai di buku-buku cetak, rangkuman, dan lain-lainnya. Bahkan ada yang sudah yang hafal. Tetapi yang jadi pertanyaan, adakah yang tau dari mana asal-usul nilai tersebut. Buat yang belum tau dari mana nilai-nilai tersebut, tanang!!! Karena pada kesempatan kali ini, penulis mencoba menjelaskan secara sederhana asal-asul nilai-nilai tersebut.

Untuk menentukan nilai-nilai perbandingan trigonometri sudut-sudut istimewa yang dimaksud, kita dapat meggunakan konsep Lingkaran Satuan. Apa itu lingkaran saatua? Lingkaran satuan adalah lingkaran yang berjari-jari satu satuan seperti pada gambar berikut.

Lingkaran satuan itulah yang akan kita pakai.

Perbandingan Trigonometri untuk sudut $0°$.

Perhatikan lingkaran satuan berikut!

Dari gambar $OP = r = 1$ maka koordinat $P(1,0)$ atau $x=1$, dan $y=0$. $OP$ berhimpit dengan sumbu $X$ dan akibatnya besar $∠XOP=0°$. Berdasarkan defenisi perbabdingan trigonometri pada segitiga siku-siku, diperoleh:

$\begin{align*}\textrm{sin}\;0°=\frac{y}{1}=\frac{0}{1}=0\end{align*}$

$\begin{align*}\textrm{cos}\;0°=\frac{x}{1}=\frac{1}{1}=1\end{align*}$

$\begin{align*}\textrm{tan}\;0°=\frac{y}{x}=\frac{0}{1}=0\end{align*}$

Jadi, nilai perbandingan trigonometri sin $0°$, cos $0°$, dan tan $0°$ berturut-turut adalah $0$, $1$, dan $0$.

Perbandingan trigonometri untuk sudut $30°$

Perhatikan gambar berikut!

Perhatika $\triangle OPP'$, siku-siku di $P'$. Besar $\angle POP'=30^{\circ}$, maka besar $\angle OPP'=60^{\circ}$. Perhatikan $\triangle OP'Q$, dimana $\triangle OP'Q$ adalah hasil pencerminan $\triangle OPP'$ terhadap sumbu $X$ sehingga $\triangle OPP'$ dan $\triangle OP'Q$ kongruen. Oleh karena kongruen, maka $\angle POQ=\angle OPQ=\angle OQP=60^{\circ}$, dan $OP=OQ=PQ=1$. $P'$ adalah titik tengah $PQ$, maka $PP'=\frac{1}{2}PQ=\frac{1}{2}$. Panjang $OP$ dapat ditentukan dengan menggunakan Teorema Pythagoras, sebagai berikut.

$\begin{align*} (OP')^{2}&=(OP)^{2}-(PP')^{2}\\ (OP')^{2}&=1^{2}-\left(\frac{1}{2}\right )^{2}\\ (OP')^{2}&=1-\frac{1}{4}\\ (OP')^{2}&=\frac{3}{4}\\ OP'&=\sqrt{\frac{3}{4}}\\ OP'&=\frac{1}{2}\sqrt{3} \end{align*}$ 

Jadi, panjang $\begin{align*} OP'&=\frac{1}{2}\sqrt{3} \end{align*}$. Dengan demikian:

$\begin{align*}\textrm{sin}\;30°=\frac{PP'}{OP}=\frac{\frac{1}{2}}{1}=\frac{1}{2}\end{align*}$

$\begin{align*}\textrm{cos}\;30°=\frac{OP'}{OP}=\frac{\frac{1}{2}\sqrt{3}}{1}=\frac{1}{2}\sqrt{3}\end{align*}$

$\begin{align*}\textrm{tan}\;30°=\frac{PP'}{OP'}=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{3}}=\frac{1}{3}\sqrt{3}\end{align*}$

Jadi, nilai dari sin $30°$, cos $30°$, dan tan $30°$ berturut-turut adalah $\begin{align*}\frac{1}{2}\end{align*}$, $\begin{align*}\frac{1}{2}\sqrt{3}\end{align*}$, dan $\begin{align*}\frac{1}{3}\sqrt{3}\end{align*}$.

Perbandingan trigonometri sudut $45^{\circ}$ 

Perhatikan gambar berikut!

Perhatikan $\triangle OP'P$, siku-siku di $P'$. Besar $\angle POP'=45^{\circ}$, $\angle OP'P=90^{\circ}$, dan $\angle OPP'=45^{\circ}$. Oleh karena $\angle POP'=OPP'=45^{\circ}$, maka segitiga $OP'P$ adalah segitiga siku-siku sama kaki, yaitu $OP'=PP'$. Panjang $OP'$ atau $PP'$ dapat ditentukan dengan teorema pythagoras seperti berikut.

$\begin{align*}(OP')^{2}+(PP')^{2}&=(OP)^{2}\\ (PP')^{2}+(PP')^{2}&=1^{2}\\ 2(PP')^{2}&=1\\ (PP')^{2}&=\frac{1}{2}\\ PP'&=\frac{1}{2}\sqrt{2} \end{align*}$ 

Dengan demikian $\begin{align*}OP'=PP'&=\frac{1}{2}\sqrt{2} \end{align*}$.

Selanjutnya, akan kita tentukan perbandingan trigonometri untuk sudut $45^{\circ}$, sebagai berikut.

$\begin{align*}\textrm{sin}\;45^{\circ}=\frac{PP'}{OP}=\frac{\frac{1}{2}}{1}=\frac{1}{2}\end{align*}$ 

$\begin{align*}\textrm{cos}\;45^{\circ}=\frac{OP'}{OP}=\frac{\frac{1}{2}}{1}=\frac{1}{2}\end{align*}$ 

$\begin{align*}\textrm{tan}\;45^{\circ}=\frac{PP'}{OP'}=\frac{\frac{1}{2}}{\frac{1}{2}}=1\end{align*}$

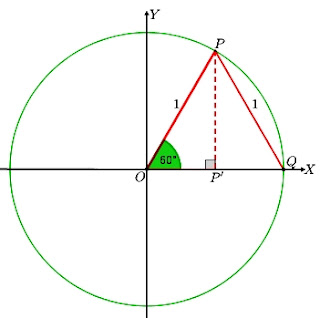
Perbandingan trigonometri untuk sudut $60°$

Perhatikan gambar berikut!

Besar $\angle POP'=60^{\circ}$, dan $P'$ adalah proyeksi titik $P$ pada sumbu $X$ sehingga besar $\angle OP'P=90^{\circ}$, dan $\angle OPP'=30^{\circ}$. Oleh karena $OP=OQ=1$, maka $\triangle OPQ$ adalah segitiga sama sisi, sehingga $P'$ adalah titik tengah $OQ$. Dengan demikian $\begin{align*}OP'=\frac{1}{2}\end{align*}$. Panjang $PP'$ dapat ditentukan dengan teorema pythagoras, sebagai berikut.

$\begin{align*}(PP')^{2}&=(OP)^{2}-(OP')^{2}\\(PP')^{2}&=1^{2}-\left(\frac{1}{2}\right)^{2}\\(PP')^{2}&=1-\frac{1}{4}\\(PP')^{2}&=\frac{3}{4}\\PP'&=\frac{1}{2}\sqrt{3}\end{align*}$

Selanjutnya, nilai perbandingan trigonometri untuk sudut $60^{\circ}$ sebagai berikut:

$\begin{align*}\textrm{sin}\;60^{\circ}=\frac{PP'}{OP}=\frac{\frac{1}{2}\sqrt{3}}{1}=\frac{1}{2}\sqrt{3}\end{align*}$

$\begin{align*}\textrm{cos}\;60^{\circ}=\frac{OP'}{OP}=\frac{\frac{1}{2}}{1}=\frac{1}{2}\end{align*}$
$\begin{align*}\textrm{tan}\;60^{\circ}=\frac{PP'}{OP}=\frac{\frac{1}{2}\sqrt{3}}{\frac{1}{2}}=\sqrt{3}\end{align*}$
Jadi, nilai dari sin $60^{\circ}$, cos $60^{\circ}$, dan tan $60^{\circ}$ berturut-turut adalah $\begin{align*}\frac{1}{2}\sqrt{3},\;\frac{1}{2}\end{align*}$, dan $\begin{align*}\sqrt{3}\end{align*}$.

Perbandingan trigonometri untuk sudut $60°$

Perhatikan gambar berikut!

Jika besar sudut yang dibentuk oleh $OP$ dengan sumbu $X$ adalah $90^{\circ}$, maka $OP$ berhimpit dengan sumbu $Y$ seperti tampak gambar.  Dengan demikian koordinat titik $P$ adalah $(0,1)$ atau nilai $x=0$, dan $y=OP=1$. Perbandingan trigonometri untuk sudut $90^{\circ}$, sebagai berikut.

$\begin{align*}\textrm{sin}\;90^{\circ}=\frac{y}{OP}=\frac{1}{1}=1\end{align*}$ 

$\begin{align*}\textrm{cos}\;90^{\circ}=\frac{x}{OP}=\frac{0}{1}=0\end{align*}$ 

$\begin{align*}\textrm{tan}\;90^{\circ}=\frac{y}{x}=\frac{1}{0}=\textrm{tak terdefenisi}\end{align*}$

Jadi, nilai dari sin $90^{\circ}$, cos $90^{\circ}$, dan tan $90^{\circ}$ berturut-turut adalah $1$, $0$, dan tak terdefenisi.

Dari uraian di atas, nilai-nilai perbandingan trigonomotri untuk sudut $0°$, $30°$, $45°$, $60°$, dan $90°$ dapat dirangkum seperti tabel berikut.

Selanjutnya, nilai-nilai perbandingan trigonometri sudut-sudut istimewa tersebut dapat digunakan untuk menentukan panjang (ukuran) sisi dari suatu segitiga siku-siku, tinggi suatu gedung, tinggi pohon dan lain sebagainya. Untuk lebih jelasnya, perhatikan beberapa contoh soal berikut.

Contoh 1
Perhatikan gambar berikut!

Jika besar $\angle A=30^{\circ}$, $BC=12$ cm, tentukan panjang $AB$ dan $AC$.

Pembahasan

Panjang $AB$

$\begin{align*} \textrm{tan}\;\angle A&=\frac{BC}{AB}\\ \textrm{tan}\;30^{\circ}&=\frac{12}{BC}\\ \frac{1}{3}\sqrt{3}&=\frac{12}{AB}\\ AB\sqrt{3}&=36\\ AB&=\frac{36}{\sqrt{3}}\\ AB&=12\sqrt{3} \end{align*}$

Panjang $AC$

$\begin{align*} \textrm{sin}\;\angle A&=\frac{BC}{AC}\\ \textrm{sin}\;30^{\circ}&=\frac{12}{AC}\\ \frac{1}{2}&=\frac{12}{AC}\\ AC&=24 \end{align*}$

Jadi, panjang $AB$ dan $AC$ berturut-turut adalah$\begin{align*} 12\sqrt{3} \end{align*}$ cm dan $24$ cm.

Contoh 2
Perhatikan gambar di bawah ini.

Jika panjang $BC=10$ cm, maka panjang $AB=....$ cm.(A). $10\sqrt{3}-5$
(B). $15-10\sqrt{3}$
(C). $6\sqrt{3}-3$
(D). $10\sqrt{3}-5$
(E). $10(\sqrt{3}-1)$
Pembahasan
Panjang $CD$
Perhatikan segitiga siku-siku $BCD$.

$\begin{align*} \textrm{tan}\angle B&=\frac{CD}{BC}\\ \textrm{tan}\;45^{\circ}&=\frac{CD}{10}\\ 1&=\frac{CD}{10}\\ CD&=10 \end{align*}$

Perhatikan segitiga $ACD$.
Misalkan panjang $AB=x$, maka $AC=(10+x)$ cm.

$\begin{align*} \textrm{tan}\angle A&=\frac{CD}{AC}\\ \textrm{tan}\;30^{\circ}&=\frac{10}{10+x}\\ \frac{1}{3}\sqrt{3}&=\frac{10}{10+x}\\ (10+x)\sqrt{3}&=30\\ 10\sqrt{3}+x\sqrt{3}&=30\\ x&=\frac{30-10\sqrt{3}}{\sqrt{3}}\\ x&=\frac{30\sqrt{3}-30}{3}\\ x&=10\sqrt{3}-10\\ x&=10(\sqrt{3}-1) \end{align*}$

Jadi, panjang $AB=10(\sqrt{3}-1)$ cm.

Contoh 3
Perhatikan gambar di bawah ini.

Diketahui $\angle BAD=30^{\circ}$,  $\angle BCD=45^{\circ}$, dan $AB=10$ cm. Tentukan panjang $CD$.
Pembahasan
Panjang $BD$
Perhatikan $\triangle BAD$,berlaku:

$\begin{align*} \textrm{sin}\angle A&=\frac{BD}{AB}\\ \textrm{sin}\;30^{\circ}&=\frac{BD}{10}\\ \frac{1}{2}&=\frac{BD}{10}\\ BD&=\frac{10\times 1}{2}\\ BD&=5 \end{align*}$ 

Selanjutnya, perhatikan $\triangle BCD$, akan ditentukan panjang $CD$ sebagai berikut.

$\begin{align*} \textrm{sin}\angle C&=\frac{BD}{CD}\\ \textrm{sin}\;45^{\circ}&=\frac{5}{CD}\\ \frac{1}{2}\sqrt{2}&=\frac{5}{CD}\\ CD\sqrt{2}&=2\times 5\\ CD&=\frac{10}{\sqrt{2}}\\ CD&=5\sqrt{2} \end{align*}$

Jadi, panjang $CD=5\sqrt{2}$

Contoh 4
Perhatikan gambar berikut!

Baca Juga

Gambar di atas menunjukkan seorang anak berada pada jarak $32$ meter dari kaki sebuah gedung. Ia melihat puncak gedung dan helicopter dengan sudut elevasi masing-masing $30°$ dan $45°$. Hitunglah tinggi helicopter tersebut dari atas gedung.

Pembahasan

Ketinggian pesawat dari atas gedung adalah panjang $CD$.
Perhatikan segitiga $ABC$, $\angle BAC=30^{\circ}$, maka:

$\begin{align*} \textrm{tan}\angle BAC&=\frac{BC}{AB}\\ \textrm{tan}\;30^{\circ}&=\frac{BC}{32}\\ \frac{1}{3}\sqrt{3}&=\frac{BC}{32}\\ BC&=\frac{32}{3}\sqrt{3} \end{align*}$

Selanjutnya, perhatikan segitiga $ABD$, $\angle BAD=45^{\circ}$, maka:

$\begin{align*} \textrm{tan}\angle BAD&=\frac{BD}{AB}\\ \textrm{tan}\;45^{\circ}&=\frac{BD}{32}\\ 1&=\frac{BD}{32}\\ BD&=32 \end{align*}$ 

Tinggi pesawat = $BD-BC$, yaitu sebagai berikut.

$\begin{align*}CD&=BD-BC\\ CD&=32-\frac{32\sqrt{3}}{3}\\ CD&=32\left(1-\frac{1}{3}\sqrt{3} \right ) \end{align*}$ 

Jadi, tinggi pesawat dari atas gedung $\begin{align*}32\left(1-\frac{1}{3}\sqrt{3} \right ) \end{align*}$ meter.

Contoh 5
Tentukan nilai dari: $\displaystyle \begin{align*} \textrm{sin}\;60^{\circ}\times \textrm{cos}\;30^{\circ}-\textrm{cos}\;60^{\circ}\times \textrm{sin}\;30^{\circ} \end{align*}$
Pembahasan
$\displaystyle \begin{align*} \textrm{sin}\;60^{\circ}\times \textrm{cos}\;30^{\circ}-\textrm{cos}\;60^{\circ}\times \textrm{sin}\;30^{\circ}&=\frac{1}{2}\sqrt{3}\times \frac{1}{2}\sqrt{3}-\frac{1}{2}\times \frac{1}{2}\\ &=\frac{3}{4}-\frac{1}{4}\\ &=\frac{2}{4}\\ &=\frac{1}{2} \end{align*}$

Contoh 6
Tentukan nilai dari: $\begin{align*}\frac{\textrm{sin}\;30^{\circ}-\textrm{tan}\;30^{\circ}+\textrm{cos}\;30^{\circ}}{\textrm{tan}\;60^{\circ}-\textrm{sin}\;45^{\circ}+\textrm{cos}\;45^{\circ}} \end{align*}$
Pembahasan
$\begin{align*}\frac{\textrm{sin}\;30^{\circ}-\textrm{tan}\;30^{\circ}+\textrm{cos}\;30^{\circ}}{\textrm{tan}\;60^{\circ}-\textrm{sin}\;45^{\circ}+\textrm{cos}\;45^{\circ}}&=\frac{\frac{1}{2}-\frac{1}{3}\sqrt{3}+\frac{1}{2}}{\sqrt{3}-\frac{1}{2}\sqrt{2}+\frac{1}{2}\sqrt{2}}\\ &=\frac{1-\frac{1}{3}\sqrt{3}}{\sqrt{3}}\\ &=\frac{\sqrt{3}-1}{3}\end{align*}$

Demikianlah yang bisa penulis bagikan. Apabila ditemukan kesalahan dan keliruan segera dikomentari di kolom komentar agar dapat diperibaiki. Semoga bermanfaat.