Kedudukan Titik Terhadap Lingkaran

Kedudukan Titik Terhadap Lingkaran

Dalam kasus ini yaitu kedudukan suatu titik terhadap lingkaran dapat dibedakan menjadi tiga kondisi,yaitu titik terletak di dalam lingkaran, titik terletak pada lingkaran,dan titik di luar lingkaran.
Kedudukan suatu titik terhadap lingkaran dapat dibedakan berdasarkan persamaan lingkaran.

a. Kedudukan titik terhadap lingkaran dengan persamaan $x^{2} + y^{2}=r^{2}$

Misalkan titik $P(x_{1},y_{1})$,maka kedudukan titik $P$ terhadap lingkaran $x^{2}+y^{2}=r^{2}$ adalah sebagai betikut.

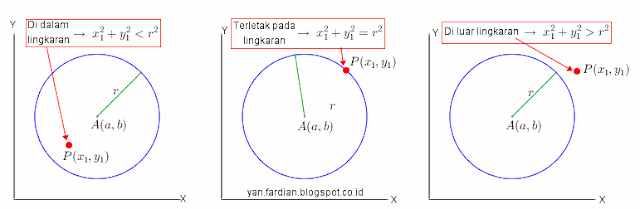
$(a)$ Titik $P(x_{1},y_{1})$ bearada di dalam lingkaran $x^{2} + y^{2}=r^{2}$ jika:

$x_{2}^{2}+y_{1}^{2}<r^{2}$

$(b)$ Titik $P(x_{1},y_{1})$ berada tepat pada lingkaran $x^{2} + y^{2}=r^{2}$ jika:

$x_{1}^{2}+y_{1}^{2}=r^{2}$

$(c)$ Titik $P(x_{1},y_{1})$ terletak di luar lingkaran $x^{2} + y^{2}=r^{2}$ jika:

$x_{1}^{2}+y_{1}^{2}>r^{2}$

Letak ketiga titik tersebut seperti ditunjukkan oleh gambar berikut.

Kedudukan titik $P$ terhadap lingakaran $x^{2}+y^{2}=r^{2}$

b. Kedudukan titik terhadap lingkaran dengan persamaan $x^{2}+y^{2}+Ax+By+C=0$

Misalkan titik $P(x_{1},y_{1})$, maka kedudukan titik $P$ terhadap lingkaran $x^{2}+y^{2}+Ax+By+C=0$ adalah sebagai berikut.

$(a)$  Titik $P(x_{1},y_{1})$ terletak di dalam lingkaran $x^{2}+y^{2}+Ax+By+C=0$ jika:

$x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C<0$

$(b)$ Titik $P(x_{1},y_{1})$ terletak di dalam lingkaran $x^{2}+y^{2}+Ax+By+C=0$ jika:

$x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C=0$

$(c)$ Titik $P(x_{1},y_{1})$ terletak di dalam lingkaran $x^{2}+y^{2}+Ax+By+C=0$ jika:

$x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C>0$

Supaya lebih jelas, perhatikanlah gambar berikut.

Kedudukan titik $P$ terhadap lingkara $x^{2}+y^{2}+Ax+By+C=0$

Perhatikanlah beberapa contoh soal berikut.

CONTOH SOAL  1

Tentukan kedudukan (posisi) titik-titik berikut terhadap lingkaran $x^{2}+y^{2}=25$

a. $(3,1)$              b. $(4,-3)$              c. $(-2,-5)$

Jawab 
$\begin{align*} \textrm{a}.\;(3,1)\;&\Leftrightarrow \;x_{1}^{2}+y_{1}^{2}=(3)^{2}+(1)^{2} \\ &\Leftrightarrow x_{1}^{2}+y_{1}^{2}=10 \end{align*}$

Karena $x_{1}^{2}+y_{1}^{2}<25$, maka titik $(3,1)$ terletak di dalam lingkaran $x^{2}+y^{2}=25$.

$\begin{align*} \textrm{b}.\;(4,-3)\;&\Leftrightarrow \; x_{1}^{2}+y_{1}^{2}=(4)^{2}+(-3)^{2} \\ &\Leftrightarrow x_{1}^{2}+y_{1}^{2}=25 \end{align*}$

Karena $\begin{align*} x_{1}^{2}+y_{1}^{2}>25 \end{align*}$ , maka titik $(4,-3)$ terletak pada lingkaran $x^{2}+y^{2}=25$

Baca Juga

$\begin{align*} \textrm{C}.\;(-2,-5)\;&\Leftrightarrow \; x_{1}^{2}+y_{1}^{2}=(-2)^{2}+(-5)^{2} \\ &\Leftrightarrow x_{1}^{2}+y_{1}^{2}=29 \end{align*}$  

Karena $\begin{align*} x_{1}^{2}+y_{1}^{2}>25 \end{align*}$ , maka titik $(-2,-5)$ terletak di luar lingkaran $x^{2}+y^{2}=25$

CONTOH SOAL  2

Tentukan kedudukan (posisi) titik $(-2,9)$ terhadap lingkaran$x^{2}+y^{2}+4x-8y-5=0$.

Jawab
Substitusi titik $(-2,9)$ ke dalam persamaan lingkaran.
$\begin{align*} &x_{1}^{2}+y_{1}^{2}+4x-8y-5\\ &=(-2)^{2}+(9)^{2}+4(-2)-8(9)-5 \\ &=4+81-8-72-5\\ &=0 \end{align*}$  
Karena$\begin{align*} x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C=0 \end{align*}$,maka titik $(-2,9)$ terletak pada lingkaran $x^{2}+y^{2}+4x-8y-5=0$.

CONTOH SOAL  3

Tentukanlah nilai $m$ agar titik $(-5,m)$ terletak pada lingkaran$x^{2}+y^{2}+2x-5y-21=0$. 

Jawab
Misalkan $P(-5,m)$ maka $x_{1}=-5$ dan $y_{1}=m$. Agar titik $P$ terletak pada lingkaran tersebut maka syarat yang harus dipenuhi adalah:

$x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C=0$

Sehingga:

$\begin{align*}x_{1}^{2}+y_{1}^{2}+Ax_{1}+By_{1}+C&=0\\(-5)^{2}+(m)^{2}+2(-5)-5(m)-21&=0\\25+m^{2}-10-5m-21&=0\\m^{2}-5m-6&=0\\(m+1)(m-6)&=0\\m=-1\;\;atau\;\;m&=6\end{align*}$

Jadi, nilai $m=-1$ dan $m=6$.

CONTOH SOAL  4

Tentukanlah persamaan lingkaran yang pusatnya $(4,3)$ dan melalui titik $(2,-2)$.

Jawab
Misalkan persamaan lingkaran tersebut $(x-a)^{2}+(y-b)^{2}=0$
Substitusi titik $(4,3)$ dan $(2,-2)$ ke persamaan diperoleh:
$\begin{align*}(x-a)^{2}+(y-b)^{2}&=r^{2}\\(2-4)^{2}+(-2-3)^{2}&=r^{2}\\4+25&=r^{2}\\29&=r^{2}\end{align*}$

Persamaan lingkaran dengan pusat $(4,3)$ dapat ditentukan.
$\begin{align*}(x-4)^{2}+(y-3)^{2}&=r^{2}\\x^{2}-8x+16+y^{2}-6y+9&=29\\x^{2}+y^{2}-8x-6y-4&=0\end{align*}$
Jadi,persamaan lingkarannya $x^{2}+y^{2}-8x-6y-4=0$.

CONTOH SOAL  5

Tentukanlah persamaan lingkaran yang melalui titik-titik $K(2,7)$, $L(-5,6)$  dan $M(3,0)$.

Jawab
Misalkan persamaan lingkaran yang diminta adalah $x^{2}+y^{2}+Ax+By+C=0$. Karena $K$, $L$, dan $M$ terletak (melalui) lingkaran maka koordinat ketiga titik tersebut haruslah memenuhi persamaan lingkaran. Substitusi ketiga titik tersebut ke persamaan pemisalan.

Titik $K(2,7)$
$\begin{align*}2^{2}+7^{2}+A(2)+B(7)+C&=0\\2A+7B+C&=-53\;\;\;\;\;...(1)\end{align*}$

Titik $L(-5,6)$
$\begin{align*}(-5)^{2}+6^{2}+A(-5)+B(6)+C &=0\\-5A+6B+C &=0\;\;\;....(2)\end{align*}$

Titik $L(3,0)$
$\begin{align*}3^{2}+0^{2}+A(2)+B(0)+C&=0\\3A+C&=0\;\;\;\;\;....(3)\end{align*}$

Dengan menyelesaikan ketiga persamaan yang di atas,diperoleh nilai $A=2$, $B=-6$, dan $C=-15$. Jika nilai-nilai ini dimasukkan kembali ke persamaan semula akan diperoleh persamaan lingkaran yang dicari,yaiti: $x^{2}+y^{2}+2x-6y-15=0$.

CONTOH SOAL 6

Tentukanlah persamaan lingkaran yang menyinggung sumbu$-X$,mempunyai pusat pada garis $x+y-7=0$,melalui titik $(5,4)$.

Jawab
Misalkan titik pusat lingkaran yang dicari adalah $(a,b)$ dan berjari-jari $r$ maka persamaan lingkaran tersebut berbentuk:

$\begin{align*}(x-a)^{2}+(y-b)^{2}=r^{2}\;\;\;\;....(1)\end{align*}$

Karena lingkaran menyinggung sumbu$-X$,maka:

$\begin{align*}r=b\;\;\;\;\;.....(2)\end{align*}$

Karena titik pusat lingkaran $(a,b)$ terletak garis $x+y-7=0$ maka koordinat titik pusat lingkaran haruslah memenuhi persamaan garis,sehingga:

$\begin{align*}x+y-7&=0\\a+b&=7\;\;\;\;....(3)\end{align*}$

Karena titik $(5,4)$ melalui lingkaran maka diperoleh persamaan:

$\begin{align*}(x-a)^{2}+(y-b)^{2}&=r^{2}\\(5-a)^{2}+(4-b)^{2}&=b^{2}\\a^{2}-10a-8b+41&=0\;\;\;\;....(4)\end{align*}$

Persamaan $(3)$ ekuivalen dengan $b=7-a$, subatitusi ke persamaan $(4)$ diperoleh:

$\begin{align*}a^{2}-10a-8b+41&=0\\a^{2}-8a-8(7-a)+41&=0\\a^{2}-10a-56+8a+41&=0\\a^{2}-2a-15&=0\\(a-5)(a+3)&=0\\a=5\;\;\;\;atau\;\;\;a&=-3\end{align*}$

Untuk $a=5\rightarrow b=2\rightarrow r=2$

Untuk $a=-3\rightarrow b=10\rightarrow=10$

Dengan demikian ada dua kemungkinan persamaan lingkaran yang dimaksud.
Persamaan lingkaran I
Untuk $a=5$, $b=2$, dan $r=2$:
$\begin{align*}(x-a)^{2}+(y-b)^{2}&=r^{2}\\(x-5)^{2}+(y-2)^{2}&=2^{2}\\x^{2}-10x+25+y^{2}-4y+4&=4\\x^{2}+y^{2}-10x-4y+25&=0\end{align*}$

Persamaan lingkaran II
Untuk $a=-3$, $b=10$, dan $r=10$:
$\begin{align*}(x-a)^{2}+(y-b)^{2}&=0\\(x+3)^{2}+(y-10)^{2}&=10^{2}\\x^{2}+6x+9+y^{2}-20y+100&=100\\x^{2}+y^{2}+6x-20y+9&=0\end{align*}$

Jadi, persamaan lingkaran yang dicari adalah $x^{2}+y^{2}-10x-4y+25=0$ dan $x^{2}+y^{2}+6x-20y+9=0$ dan terlihat seperti gambar berikut.

Demikianlah pembahasan materi tentang Kedudukan Titik terhadap Lingkaran. Apabila ditemukan keselahan baik itu jawaban maupun pengetikan silakan dikonetari pada kolom komentar di bawah.

Semoga bermanfaat.

Salam Matematika...